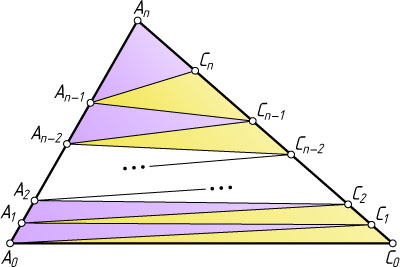
16498. Дан треугольник A_{0}C_{0}A_{n}
(см. рис.). Известно, что 2n
треугольников A_{i-1}C_{i}A_{i}
и C_{i-1}A_{i-1}C_{i}
(i=1
, 2, …, n
) равновелики. Найдите отношение \frac{A_{n}C_{n}}{A_{n}C_{0}}
.
Ответ. \frac{(2n)!}{2^{2n}\cdot(n!)^{2}}
.
Решение. У треугольников A_{0}C_{1}A_{n}
и A_{0}C_{0}A_{n}
общая высота, проведённая из вершины A_{0}
, поэтому
\frac{A_{n}C_{1}}{A_{n}C_{0}}=\frac{S_{\triangle A_{0}C_{1}A_{n}}}{S_{\triangle A_{0}C_{0}A_{n}}}=\frac{2n-1}{2n}.
Аналогично для пары треугольников A_{1}C_{2}A_{n}
и A_{1}C_{1}A_{n}
и т. д. Следовательно,
\frac{A_{n}C_{n}}{A_{n}C_{0}}=\frac{A_{n}C_{1}}{A_{n}C_{0}}\cdot\frac{A_{n}C_{2}}{A_{n}C_{1}}\dots\frac{A_{n}C_{n}}{A_{n}C_{n-1}}=\frac{2n-1}{2n}\cdot\frac{2n-3}{2n-2}\dots\frac{1}{2}=\frac{(2n)!}{2^{2n}\cdot(n!)^{2}}.
Источник: Журнал «Mathematics Magazine». — 1997, том 70, № 2, задача Q862, с. 142 и 150
