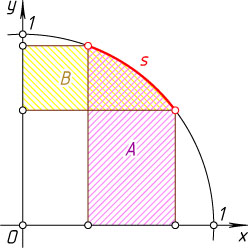
16505. Пусть s
— дуга единичной окружности, лежащая внутри первого квадранта (см. рис.), A
— площадь криволинейной трапеции, лежащей ниже s
и выше оси абсцисс, B
— площадь криволинейной трапеции, лежащей левее s
и правее оси ординат. Докажите, что сумма A+B
зависит только от длины дуги s
, и не зависит от её положения.
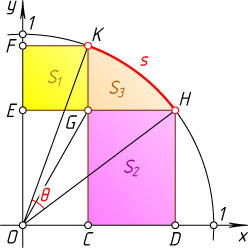
Решение. Пусть S_{1}
и S_{2}
— площади прямоугольников EGKF
и CDHG
соответственно, S_{3}
— площадь криволинейного треугольника GHK
, а S_{4}
— площадь сектора OHK
. Тогда
S_{1}=2S_{\triangle OGK}~\mbox{и}~S_{2}=2S_{\triangle OGH}.
Значит,
A+B=S_{1}+S_{2}+2S_{3}=2S_{\triangle OGK}+2S_{\triangle OGH}+2S_{3}=
=2(S_{\triangle OGK}+S_{\triangle OGH}+S_{3})=2S_{4}=2\cdot\frac{1}{2}\theta=\theta,
где \theta
— длина дуги s
. Отсюда следует утверждение задачи.
Источник: Журнал «Mathematics Magazine». — 1999, том 72, № 1, задача A-2, с. 73
Источник: Математические олимпиады США. —

