1654. На стороне AB
квадрата ABCD
взята точка E
, а на стороне CD
— точка F
, причём AE:EB=1:2
, а CF=FD
. Будут ли голубой и розовый треугольники (см.рис.) подобны?
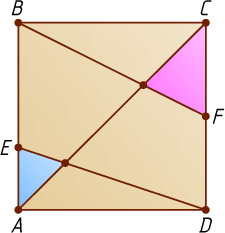
Ответ. Да.
Указание. В каждом из указанных треугольников найдите отношение сторон, заключающих угол в 45^{\circ}
, или воспользуйтесь формулой
\tg(\alpha+\beta)=\frac{\tg\alpha+\tg\beta}{1-\tg\alpha\tg\beta}.
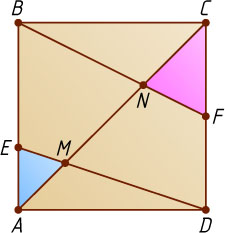
Решение. Первый способ. Пусть отрезки BF
и DE
пересекают диагональ AC
в точках N
и M
соответственно. Из подобия треугольников CNF
и ANB
следует, что CN=\frac{1}{3}AC
, а из подобия треугольников CMD
и AME
— AM=\frac{1}{4}AC
.
Если сторона квадрата ABCD
равна a
, то
CF=\frac{a}{2},~AE=\frac{a}{3},~AC=a\sqrt{2},~CN=\frac{a\sqrt{2}}{3},~AM=\frac{a\sqrt{2}}{4}.
Поэтому
\frac{AM}{AE}=\frac{\frac{a\sqrt{2}}{4}}{\frac{a}{3}}=\frac{3\sqrt{2}}{4},
\frac{CF}{CN}=\frac{\frac{a}{2}}{\frac{a\sqrt{2}}{3}}=\frac{3}{2\sqrt{2}}=\frac{3\sqrt{2}}{4}.
Поскольку \angle NCF=\angle EAM=45^{\circ}
, то треугольники CNF
и AEM
подобны.
Второй способ. Пусть отрезки BF
и DE
пересекают диагональ AC
в точках N
и M
соответственно. Тогда
\tg\angle NFC=\tg\angle BFC=\frac{BC}{CF}=2,~\tg\angle AEM=\tg\angle AED=\frac{AD}{AE}=3,
\tg\angle NCF=\tg\angle EAM=\tg45^{\circ}=1.
Поэтому
\tg\angle CNF=\tg(180^{\circ}-\angle NCF-\angle NFC)=-\tg(\angle NCF+\angle NFC)=-\frac{2+1}{1-1\cdot2}=3.
Следовательно, \angle CNF=\angle AEM
. Поэтому треугольники CNF
и AEM
подобны по двум углам.
Автор: Савин А. П.
Автор: Паравян Н. А.
Источник: Журнал «Квант». — 1986, № 1, с. 34, М961
Источник: Задачник «Кванта». — М961

