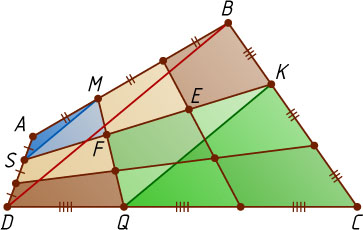
1655. Каждая сторона выпуклого четырёхугольника разделена на три равные части. Соответствующие точки деления на противоположных сторонах соединены отрезками (рис.). Докажите, что эти отрезки делят друг друга на три равные части.
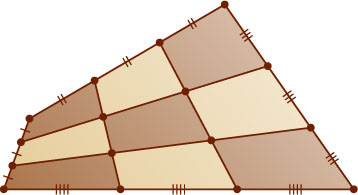
Указание. Проведите диагональ четырёхугольника. Рассмотрите образовавшиеся при этом подобные треугольники.
Решение. Обозначим указанные точки, как показано на рисунке. Докажем сначала, что SF=\frac{1}{2}FK
. Для этого соединим точки M
и S
, K
и Q
.
Из подобия треугольников MAS
и BAD
следует, что
SM\parallel BD~\mbox{и}~\frac{SM}{BD}=\frac{1}{3},
а из подобия треугольников KCQ
и BCD
—
KQ\parallel BD~\mbox{и}~\frac{KQ}{BD}=\frac{2}{3}.
Поэтому
SM\parallel KQ~\mbox{и}~\frac{SM}{KQ}=\frac{1}{2}.
Следовательно, треугольники MFS
и QFK
подобны с коэффициентом \frac{1}{2}
. Значит, \frac{SF}{FK}=\frac{1}{2}
.
Аналогично докажем, что \frac{EK}{SE}=\frac{1}{2}
. Следовательно,
SF=FE=EK.
Аналогично для остальных отрезков.