16583. Через вершину D
квадрата ABCD
проведена прямая l
, и на неё опущены перпендикуляры AX
, BY
и CZ
, как показано на рисунке. Известно, что площадь квадрата ABCD
равна 169, а AX=5
.
а) Найдите отрезок CZ
.
б) Найдите отрезок BY
.
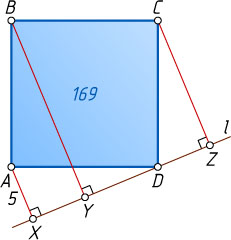
Ответ. а) 12; б) 17.
Решение. Сторона данного квадрата равна 13. Обозначим \angle ADX=\alpha
. Тогда
\angle DCZ=90^{\circ}-\angle CDZ=90^{\circ}-(90^{\circ}-\alpha)=\alpha.
Пусть прямая, проведённая через вершину A
параллельно прямой l
, пересекает отрезок BY
в точке E
. Тогда
\angle ABY=\angle DAE=\angle ADX=\alpha,
значит, прямоугольные треугольники CZD
, DXA
и BEA
равны по гипотенузе острому углу, равному \alpha
.
а) Из равенства треугольников CZD
и DXA
получаем, что
CZ=DX=\sqrt{AD^{2}-AX^{2}}=\sqrt{169-25}=\sqrt{144}=12.
б) Из равенства треугольников BEA
и DXA
получаем, что BE=DX=12
, а так как AEYX
— прямоугольник, то EY=AX=5
. Следовательно,
BY=BE+EY=12+5=17.
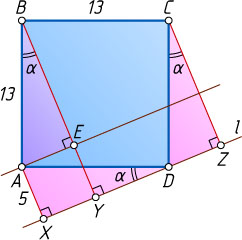
Источник: Всероссийская олимпиада школьников. — 2023-2024, 9 класс, муниципальный этап, задача 9.2

