1659. Медиана BK
и биссектриса CL
треугольника ABC
пересекаются в точке P
. Докажите равенство \frac{PC}{PL}-\frac{AC}{BC}=1
.
Указание. Через вершину C
проведите прямую, параллельную AB
.
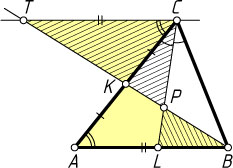
Решение. Через вершину C
проведём прямую, параллельную AB
, до пересечения с продолжением медианы BK
в точке T
. Из равенства треугольников TKC
и BKA
следует, что CT=AB
. Из подобия треугольников TPC
и BPL
находим, что
\frac{PC}{PL}=\frac{CT}{BL}=\frac{AB}{BL}=\frac{AL+LB}{BL}=\frac{AL}{BL}+1=\frac{AC}{BC}+1,
так как по свойству биссектрисы треугольника \frac{AL}{BL}=\frac{AC}{BC}
. Следовательно,
\frac{PC}{PL}-\frac{AC}{BC}=1.
Автор: Анджапаридзе З.
Источник: Журнал «Квант». — 1982, № 4, с. 25, М736
Источник: Задачник «Кванта». — М736
