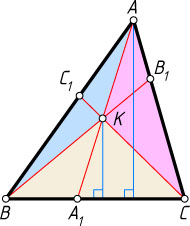
1664. Теорема Жергона. Точки A_{1}
, B_{1}
, C_{1}
лежат соответственно на сторонах BC
, AC
, AB
треугольника ABC
, причём отрезки AA_{1}
, BB_{1}
, CC_{1}
пересекаются в точке K
. Докажите, что
\frac{KA_{1}}{AA_{1}}+\frac{KB_{1}}{BB_{1}}+\frac{KC_{1}}{CC_{1}}=1~\mbox{и}~\frac{AK}{AA_{1}}+\frac{BK}{BB_{1}}+\frac{CK}{CC_{1}}=2.
Указание. Примените метод площадей.
Решение. Поскольку высоты треугольников BKC
и ABC
, опущенные на общее основание BC
, относятся, как отрезки KA_{1}
и AA_{1}
то
\frac{S_{\triangle BKC}}{S_{\triangle ABC}}=\frac{KA_{1}}{AA_{1}}.
Аналогично
\frac{S_{\triangle AKC}}{S_{\triangle ABC}}=\frac{KB_{1}}{BB_{1}},~\frac{S_{\triangle AKB}}{S_{\triangle ABC}}=\frac{KC_{1}}{CC_{1}}.
Поэтому
\frac{KA_{1}}{AA_{1}}+\frac{KB_{1}}{BB_{1}}+\frac{KC_{1}}{CC_{1}}=\frac{S_{\triangle BKC}}{S_{\triangle ABC}}+\frac{S_{\triangle AKC}}{S_{\triangle ABC}}+\frac{S_{\triangle AKB}}{S_{\triangle ABC}}=
=\frac{S_{\triangle BKC}+S_{\triangle AKC}+S_{\triangle AKB}}{S_{\triangle ABC}}=\frac{S_{\triangle ABC}}{S_{\triangle ABC}}=1
Поскольку
\frac{AK}{AA_{1}}=\frac{AA_{1}-KA_{1}}{AA_{1}}=1-\frac{KA_{1}}{AA_{1}},~\frac{BK}{BB_{1}}=1-\frac{KB_{1}}{BB_{1}},~\frac{CK}{CC_{1}}=1-\frac{KC_{1}}{CC_{1}},
то
\frac{AK}{AA_{1}}+\frac{BK}{BB_{1}}+\frac{CK}{CC_{1}}=3-\left(\frac{KA_{1}}{AA_{1}}+\frac{KB_{1}}{BB_{1}}+\frac{KC_{1}}{CC_{1}}\right)=3-1=2.
Примечание. Теорема верна и для случая, когда точка K
лежит не внутри треугольника ABC
, а на его стороне (тогда одно из слагаемых обратится в 0).
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 17
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 30
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 62, с. 105
