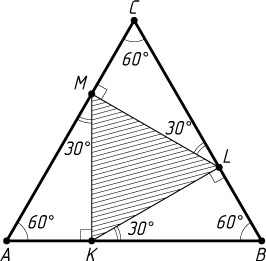
1670. На каждой стороне правильного треугольника взято по точке. Стороны треугольника с вершинами в этих точках перпендикулярны сторонам исходного треугольника. В каком отношении каждая из взятых точек делит сторону исходного треугольника?
Ответ. 1:2
.
Указание. Докажите, что треугольник KLM
также равносторонний.
Решение. Пусть точки K
, L
, M
лежат соответственно на сторонах AB
, BC
и AC
правильного треугольника ABC
, причём KL\perp BC
, LM\perp AC
, MK\perp AB
. Тогда
\angle MKL=180^{\circ}-\angle AKM-\angle LKB=180^{\circ}-90^{\circ}-30^{\circ}=60^{\circ}.
Аналогично \angle KML=60^{\circ}
. Значит, треугольник KLM
также равносторонний. Прямоугольные треугольники AKM
, BLK
и CML
равны по гипотенузе и острому углу, а так как CM=AK=\frac{1}{2}AM
, то CM:AM=1:2
. Аналогично AK:KB=BL:LC=1:2
.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 7.33, с. 67
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 7.33.1, с. 70
