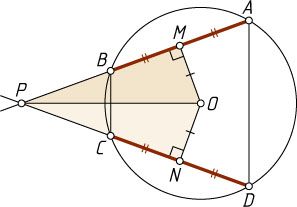
1699. Продолжения равных хорд AB
и CD
окружности соответственно за точки B
и C
пересекаются в точке P
. Докажите, что треугольники APD
и BPC
равнобедренные.
Указание. Перпендикуляры OM
и ON
, опущенные из центра O
окружности на равные хорды AB
и CD
, равны и делят эти хорды пополам.
Решение. Перпендикуляры OM
и ON
, опущенные из центра O
окружности на равные хорды соответственно AB
и CD
, равны и делят эти хорды пополам, поэтому прямоугольные треугольники POM
и PON
равны по катету и гипотенузе, значит, PM=PN
. Следовательно,
PA=PM+MA=PM+\frac{1}{2}AB=PN+\frac{1}{2}CD=PN+ND=PD,
PB=PA-AB=PD-CD=PC.