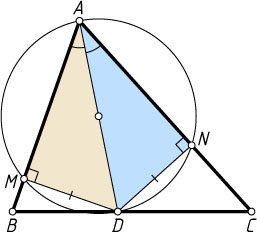
1700. Окружность, построенная на биссектрисе AD
треугольника ABC
как на диаметре, пересекает стороны AB
и AC
соответственно в точках M
и N
, отличных от A
. Докажите, что AM=AN
.
Указание. Прямоугольные треугольники AMD
и AND
равны.
Решение. Поскольку точки M
и N
лежат на окружности с диаметром AD
, то
\angle AMD=\angle AND=90^{\circ}.
Поэтому длины отрезков DM
и DN
— расстояния от точки D
, лежащей на биссектрисе угла BAC
, до сторон этого угла. Значит, DM=DN
. Прямоугольные треугольники AMD
и AND
равны по катету и гипотенузе. Следовательно, AM=AN
.