1701. Найдите внутри треугольника ABC
такую точку P
, чтобы общие хорды каждой пары окружностей, построенных на отрезках PA
, PB
и PC
как на диаметрах, были равны.
Ответ. Точка пересечения биссектрис треугольника ABC
.
Указание. Докажите, что окружности с диаметрами AP
и BP
пересекаются на стороне AB
.
Решение. Пусть C_{1}
— отличная от A
точка пересечения со стороной AB
окружности, построенной на отрезке AP
как на диаметре. Поскольку точка C_{1}
лежит на окружности с диаметром AP
, то
\angle AC_{1}P=90^{\circ}.
Если C_{2}
— отличная от B
точка пересечения со стороной AB
окружности, построенной на отрезке BP
как на диаметре, то
\angle BC_{2}P=90^{\circ}.
Из единственности перпендикуляра следует, что точки C_{1}
и C_{2}
совпадают. Аналогично докажем, что окружности с диаметрами AP
и CP
пересекаются на стороне AC
(в точке B_{1}
), а окружности с диаметрами CP
и BP
— на стороне BC
(в точке A_{1}
).
По условию PA_{1}=PB_{1}=PC_{1}
, поэтому точка P
равноудалена от всех сторон треугольника ABC
. Следовательно, P
— точка пересечения биссектрис этого треугольника.
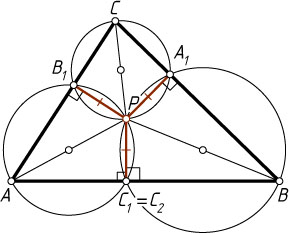
Источник: Всесибирская физико-математическая олимпиада. — 2014-2015, второй этап, задача 2, 9 класс
