1716. На сторонах четырёхугольника как на диаметрах построены четыре окружности. Докажите, общая хорда окружностей, построенных на двух соседних сторонах, параллельна общей хорде двух других окружностей, либо эти хорды лежат на одной прямой.
Указание. Окружности, построенные как на диаметрах на соседних сторонах четырёхугольника, пересекаются на его диагонали, а их общая хорда перпендикулярна этой диагонали.
Решение. Пусть окружности, построенные как на диаметрах на соседних сторонах BC
и CD
четырёхугольника ABCD
, пересекаются в точке M
. Поскольку точка M
лежит на окружности с диаметром BC
, то \angle BMC=90^{\circ}
. Аналогично \angle CMD=90^{\circ}
. Значит, точка M
лежит на диагонали BD
четырёхугольника (или на её продолжении) и CM\perp BD
. Аналогично докажем, что точка N
пересечения двух других указанных окружностей лежит на диагонали BD
(или на её продолжении) и AN\perp BD
. Следовательно, CM\parallel AN
или точки M
и N
совпадают.
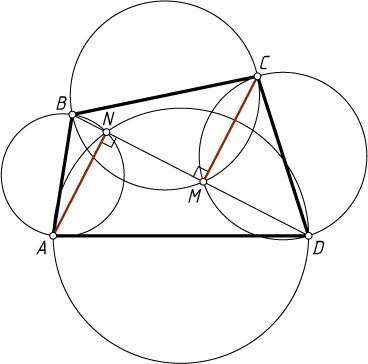
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 29, с. 32
