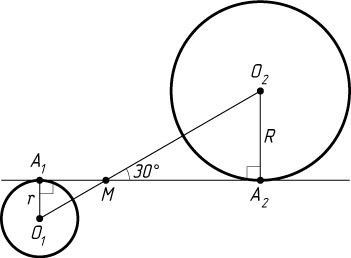
1720. Окружности, центры которых расположены по разные стороны от некоторой прямой, касаются этой прямой. Линия центров пересекает прямую под углом 30^{\circ}
. Найдите расстояние между центрами окружностей, если радиусы окружностей равны r
и R
.
Ответ. 2(r+R)
.
Указание. Катет прямоугольного треугольника, лежащий против угла 30^{\circ}
, равен половине гипотенузы.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
соответственно, A_{1}
и A_{2}
— их точки касания с данной прямой, M
— точка пересечения прямых A_{1}A_{2}
и O_{1}O_{2}
.
В прямоугольных треугольниках A_{1}O_{1}M
и A_{2}O_{2}M
углы A_{1}MO_{1}
и A_{2}MO_{2}
равны по 30^{\circ}
, поэтому
O_{1}M=2O_{1}A_{1}=2r,~O_{2}M=2A_{2}O_{2}=2R.
Следовательно,
O_{1}O_{2}=O_{1}M+O_{2}M=2(r+R).
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.7, с. 60
