1721. Угол при вершине A
треугольника ABC
равен 120^{\circ}
. Окружность касается стороны BC
и продолжений сторон AB
и AC
. Докажите, что расстояние от вершины A
до центра окружности равно периметру треугольника ABC
.
Указание. Пусть D
— точка касания окружности с прямой AB
. Докажите, что отрезок AD
равен полупериметру треугольника ABC
.
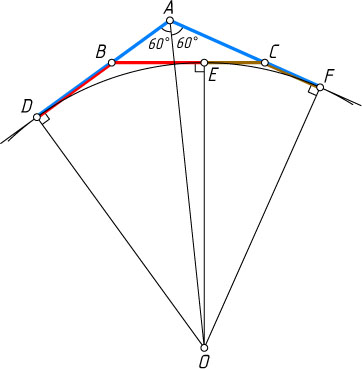
Решение. Пусть O
— центр окружности, D
, E
и F
— точки касания с прямыми AB
, BC
и AC
соответственно, 2p
— периметр треугольника ABC
. Тогда AD=AF
, BE=BD
и CE=CF
. Поэтому
2p=AB+BC+AC=AB+(BE+EC)+AC=
=(AB+BE)+(EC+AC)=(AB+BD)+(CF+AC)=AD+AF.
Значит, AD=AF=p
.
Поскольку луч AO
— биссектриса угла DAC
, то \angle DAO=60^{\circ}
. Из прямоугольного треугольника ADO
находим, что
AO=2AD=2p.