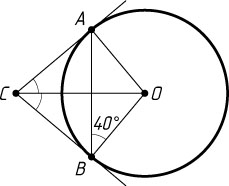
1727. Две прямые касаются окружности с центром O
в точках A
и B
и пересекаются в точке C
. Найдите угол между этими прямыми, если \angle ABO=40^{\circ}
.
Ответ. 80^{\circ}
.
Указание. CO
— биссектриса угла ACB
.
Решение. Поскольку CO
— биссектриса угла ACB
, а треугольник ABC
— равнобедренный, то CO\perp AB
. Углы ABO
и BCO
равны, так как каждый из них в сумме с углом BOC
составляет 90^{\circ}
. Следовательно,
\angle ACB=2\angle BCO=2\cdot40^{\circ}=80^{\circ}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.2, с. 60
