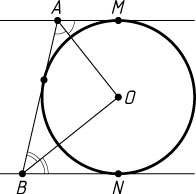
1729. Окружность касается двух параллельных прямых и их секущей. Докажите, что отрезок секущей, заключённый между параллельными прямыми, виден из центра окружности под прямым углом.
Указание. Центр окружности, вписанной в угол, лежит на биссектрисе угла.
Решение. Обозначим через A
и B
точки пересечения прямой c
с параллельными прямыми a
и b
соответственно. Пусть окружность с центром O
касается прямых a
и b
соответственно в точках M
и N
. Тогда AO
— биссектриса угла BAM
, а BO
— биссектриса угла ABN
. Поскольку \angle BAM+\angle ABN=180^{\circ}
, то
\angle BAO+\angle ABO=\frac{1}{2}\angle BAM+\frac{1}{2}\angle ABN=\frac{1}{2}(\angle BAM+\angle ABN)=\frac{1}{2}\cdot180^{\circ}=90^{\circ}.
Следовательно,
\angle AOB=180^{\circ}-(\angle BAO+\angle ABO)=90^{\circ}.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 62, с. 36
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.9, с. 60
