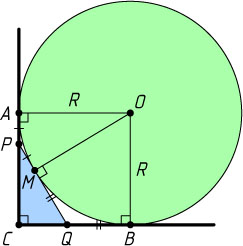
1731. В прямой угол вписана окружность радиуса R
, касающаяся сторон угла в точках A
и B
. Через некоторую точку на меньшей дуге AB
окружности проведена касательная, отсекающая от данного угла треугольник. Найдите его периметр.
Ответ. 2R
.
Указание. Примените теорему о равенстве отрезков касательных, проведённых к окружности из одной точки.
Решение. Пусть окружность с центром O
вписана в прямой угол ACB
(A
и B
— точки касания), а прямая, касающаяся окружности в точке M
, лежащей на меньшей дуге AB
, пересекает стороны CA
и CB
угла ACB
в точках P
и Q
соответственно. Тогда четырёхугольник AOBC
— квадрат. Поэтому
CP+PQ+QC=CP+(PM+MQ)+QC=(CP+PM)+(MQ+QC)=
=(CP+PA)+(MQ+QB)=CA+CB=R+R=2R.