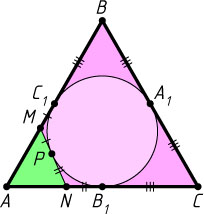
1732. К окружности, вписанной в равносторонний треугольник со стороной, равной a
, проведена касательная, пересекающая две его стороны. Найдите периметр отсечённого треугольника.
Ответ. a
.
Указание. Примените теорему о равенстве отрезков касательных, проведённых к окружности из одной точки.
Решение. Пусть окружность, вписанная в равносторонний треугольник со стороной, равной a
, касается сторон BC
, AC
и AB
в точках A_{1}
, B_{1}
и C_{1}
соответственно, а некоторая прямая пересекает стороны AB
и AC
соответственно в точках M
и N
и касается окружности в точке P
. Поскольку AC_{1}=AB_{1}
и AB=AC
, то BC_{1}=CB_{1}
, а так как BA_{1}=BC_{1}
и CA_{1}=CB_{1}
, то BA_{1}=CA_{1}
, т. е. A_{1}
— середина стороны BC
. Аналогично докажем, что C_{1}
— середина AB
и B_{1}
— середина AC
.
Поскольку MP=MC_{1}
и NP=NB_{1}
, то MN=MP+NP=MC_{1}+NB_{1}
, следовательно
AM+MN+AN=AM+(MC_{1}+NB_{1})+AN=(AM+MC_{1})+(NB_{1}+AN)=
=AC_{1}+AB_{1}=\frac{1}{2}a+\frac{1}{2}a=a.