1746. Окружность вписана в треугольник со сторонами, равными a
, b
и c
. Найдите отрезки, на которые точка касания делит сторону, равную a
.
Ответ. \frac{a+c-b}{2}
, \frac{a+b-c}{2}
.
Указание. Обозначьте один из искомых отрезков через x
и примените теорему о равенстве отрезков касательных, проведённых к окружности из одной точки.
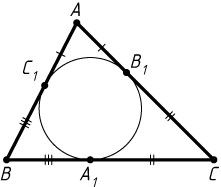
Решение. Пусть окружность касается сторон BC=a
, AC=b
и AB=c
треугольника ABC
в точках A_{1}
, B_{1}
и C_{1}
соответственно. Обозначим BA_{1}=x
. По теореме о равенстве отрезков касательных, проведённых к окружности из одной точки
BC_{1}=BA_{1}=x,~CB_{1}=CA_{1}=a-x,~AB_{1}=AC_{1}=AB-BC_{1}=c-x,
а так как AC=AB_{1}+CB_{1}
, то получим уравнение b=c-x+a-x
, откуда находим, что
BA_{1}=x=\frac{a+c-b}{2},~CA_{1}=a-x=\frac{a+b-c}{2}.
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 1, с. 6
