1763. Две окружности касаются друг друга внутренним образом. Известно, что два радиуса большей окружности, угол между которыми равен 60^{\circ}
, касаются меньшей окружности. Найдите отношение радиусов окружностей.
Ответ. 1:3
.
Указание. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
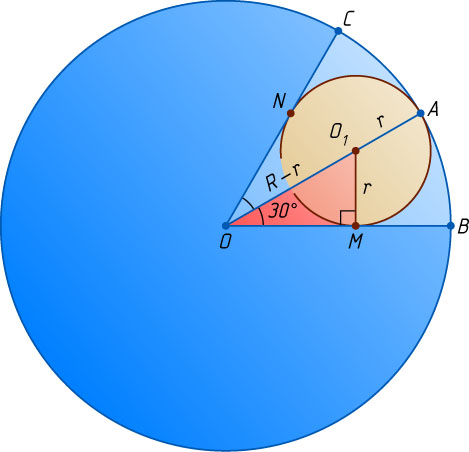
Решение. Пусть окружности с центрами O
и O_{1}
и радиусами R
и r
(R\gt r
) соответственно касаются внутренним образом в точке A
, а радиусы OB
и OC
большей окружности касаются меньшей соответственно в точках M
и N
, причём \angle BOC=60^{\circ}
.
Поскольку центр окружности, вписанной в угол, лежит на биссектрисе этого угла, \angle AOB=30^{\circ}
, а так как линия центров двух касающихся окружностей проходит через точку их касания, то
OO_{1}=OA-O_{1}A=R-r.
Из прямоугольного треугольника OO_{1}M
находим, что
OO_{1}=2O_{1}M,~\mbox{или}~R-r=2r,
откуда \frac{r}{R}=\frac{1}{3}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.12, с. 68
