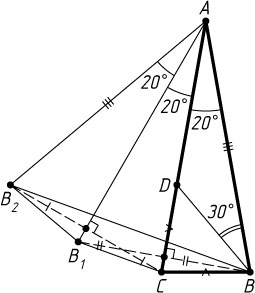
1801. Угол при вершине равнобедренного треугольника равен 20^{\circ}
. Докажите, что боковая сторона больше удвоенного основания, но меньше утроенного.
Решение. На боковой стороне AC
данного равнобедренного треугольника ABC
отложим отрезок CD
, равный основанию BC
. Тогда
\angle ABD=80^{\circ}-50^{\circ}=30^{\circ},
значит, в треугольнике ABD
угол ABD
больше угла BAD
, поэтому AD\gt BD\gt BC
(в равнобедренном треугольнике BDC
основание BD
лежит против большего угла C
). Следовательно,
AC=AD+CD\gt BC+CD=2BC.
Пусть точка B_{1}
симметрична точке B
относительно прямой AC
, а точка B_{2}
симметрична C
относительно AB_{1}
. Тогда
\angle BAB_{1}=3\angle BAC=60^{\circ},~AB_{2}=AB,
поэтому треугольник BAB_{2}
— равносторонний. Следовательно,
AB=BB_{2}\lt BC+CB_{1}+B_{1}B_{2}=3BC.