1809. Дан равнобедренный треугольник ABC
с вершиной A
. Длина прыжка кузнечика равна основанию BC
. Известно, что начиная движение из точки C
, кузнечик за 22 прыжка оказался в точке A
, приземляясь после каждого прыжка на боковой стороне треугольника ABC
и чередуя стороны при каждом прыжке, кроме последнего. Найдите углы треугольника ABC
, если известно, что с каждым прыжком кузнечик приближался к точке A
.
Ответ. 4^{\circ}
, 88^{\circ}
, 88^{\circ}
.
Указание. Примените теорему о внешнем угле треугольника.
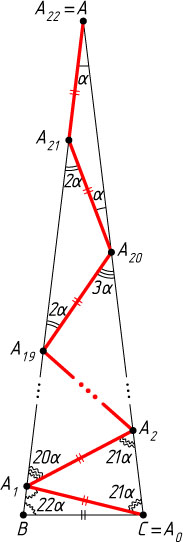
Решение. Обозначим через A_{0}
, A_{1}
, A_{2}
, …, A_{22}
точки, в которых побывал кузнечик (A_{0}
— это точка C
, A_{22}
— точка A
). Перед последним прыжком кузнечик оказался в точке A_{21}
стороны AB
. Если \angle BAC=\alpha
, то \angle A_{20}A_{21}B=2\alpha
как внешний угол равнобедренного треугольника AA_{21}A_{20}
, а так как
\angle A_{20}A_{19}A_{21}=\angle A_{20}A_{21}B=2\alpha,
то \angle A_{19}A_{20}C=3\alpha
. Рассуждая аналогично, найдём, что
\angle ACB=\angle ABC=\angle BA_{1}C=22\alpha.
Поэтому
22\alpha+22\alpha+\alpha=180^{\circ}.
Откуда
\alpha=\frac{180^{\circ}}{45}=4^{\circ}.
Автор: Гордин Р. К.
