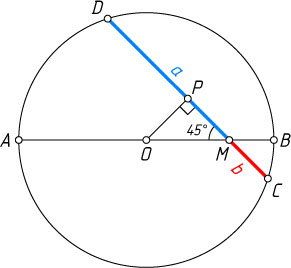
1811. Хорда окружности пересекает некоторый диаметр под углом 45^{\circ}
и делится им на отрезки, равные a
и b
. Найдите расстояние от центра окружности до этой хорды.
Ответ. \frac{1}{2}|a-b|
.
Указание. Опустите перпендикуляр из центра окружности на данную хорду.
Решение. Пусть AB
— диаметр окружности с центром O
, CD
— хорда, пересекающая диаметр AB
в точке M
, \angle AMD=45^{\circ}
, DM=a
, CM=b
. Предположим, что a\gt b
.
Опустим перпендикуляр OP
из центра окружности на хорду CD
. Поскольку диаметр, перпендикулярный хорде, делит её пополам, P
— середина CD
. В прямоугольном треугольнике OPM
известен катет
PM=DM-DP=a-\frac{1}{2}(a+b)=\frac{1}{2}(a-b)
и \angle OMP=45^{\circ}
. Следовательно,
OP=PM=\frac{1}{2}(a-b).
Аналогично для a\lt b
. Если же a=b
, то хорда CD
проходит через точку O
, т. е. является диаметром. В этом случае искомое расстояние равно 0.