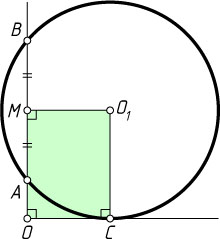
1814. Окружность касается одной стороны прямого угла с вершиной O
и пересекает вторую сторону в точках A
и B
. Найдите радиус окружности, если OA=a
и OB=b
.
Ответ. \frac{a+b}{2}
.
Указание. Опустите перпендикуляр из центра окружности на AB
.
Решение. Пусть O_{1}
— центр окружности, C
— точка касания окружности с первой стороной угла. Предположим, что a\lt b
. Поскольку перпендикуляр O_{1}M
, опущенный из центра окружности на хорду AB
, делит эту хорду пополам, то
OM=OA+\frac{1}{2}(OB-OA)=\frac{1}{2}(OA+OB)=\frac{1}{2}(a+b),
а так как O_{1}C\perp OC
, то OCO_{1}M
— прямоугольник. Следовательно,
O_{1}C=OM=\frac{1}{2}(a+b).
Аналогично для a\gt b
.