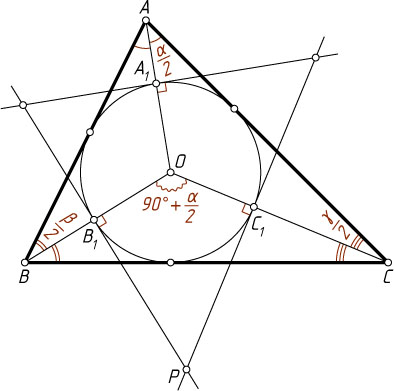
1815. Окружность с центром O
вписана в треугольник ABC
. Через точки пересечения окружности с отрезками AO
, BO
и CO
проведены к ней касательные. Найдите углы треугольника, образованного этими касательными, если углы треугольника ABC
равны \alpha
, \beta
и \gamma
.
Ответ. 90^{\circ}-\frac{\alpha}{2}
, 90^{\circ}-\frac{\beta}{2}
, 90^{\circ}-\frac{\gamma}{2}
.
Указание. \angle BOC=90^{\circ}+\frac{1}{2}\angle BAC
.
Решение. Поскольку BO
и CO
— биссектрисы углов при вершинах B
и C
данного треугольника, то
\angle BOC=90^{\circ}+\frac{1}{2}\angle BAC=90^{\circ}+\frac{\alpha}{2}
(см. задачу 4770). Пусть отрезки BO
и CO
пересекают окружность, вписанную в треугольник ABC
, в точках B_{1}
и C_{1}
, а касательные к этой окружности, проведённые через точки B_{1}
и C_{1}
, пересекаются в точке P
. Тогда сумма углов BOC
и B_{1}PC_{1}
равна 180^{\circ}
. Следовательно,
\angle B_{1}PC_{1}=180^{\circ}-\angle BOC=180^{\circ}-\left(90^{\circ}+\frac{\alpha}{2}\right)=90^{\circ}-\frac{\alpha}{2}.
Аналогично для остальных углов.