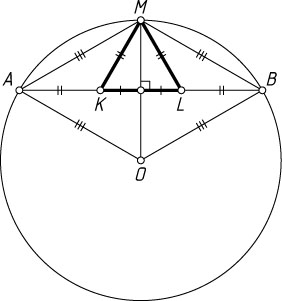
1817. Одна вершина правильного треугольника лежит на окружности, а две другие делят некоторую хорду на три равные части. Под каким углом видна хорда из центра окружности?
Ответ. 120^{\circ}
.
Указание. Пусть вершина M
данного правильного треугольника лежит на окружности центром O
, а остальные вершины на хорде AB
. Докажите, что треугольник AMO
— равносторонний.
Решение. Пусть вершина M
правильного треугольника KLM
лежит на окружности, а вершины K
и L
на хорде AB
, причём AK=KL=LB
. Поскольку AKM
и BLM
— равные равнобедренные треугольники, точка M
равноудалена от концов отрезка AB
, а так как центр O
окружности также равноудалён от концов этого отрезка, то MO
— серединный перпендикуляр к AB
. Значит, MO
— биссектриса угла AMB
, равного 120^{\circ}
. Тогда \angle AMO=60^{\circ}
, а треугольник AMO
— равносторонний. Следовательно,
\angle AOB=2\angle AOM=120^{\circ}.