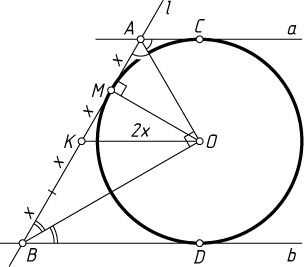
1818. Окружность касается двух параллельных прямых и их секущей. Отрезок секущей, заключённый между параллельными прямыми делится точкой касания в отношении 1:3
. Под каким углом секущая пересекает каждую из параллельных прямых?
Ответ. 60^{\circ}
.
Указание. Отрезок секущей, заключённый между параллельными прямыми, виден из центра окружности под прямым углом.
Решение. Пусть прямая l
пересекает данные параллельные прямые a
и b
соответственно в точках A
и B
, а окружность с центром O
касается прямых a
, b
и l
соответственно в точках C
, D
и M
. Поскольку OA
и OB
— биссектрисы углов CAB
и ABD
, а сумма этих углов равна 180^{\circ}
, то \angle AOB=90^{\circ}
.
Проведём медиану OK
прямоугольного треугольника AOB
. Обозначим AM=x
. Тогда
BM=3x,~OK=AK=BK=2x,~KM=AK-AM=2x-x=x=AM.
Поэтому высота OM
треугольника AOK
является его медианой. Значит, AO=OK=AK
, т. е. треугольник AOK
— равносторонний. Следовательно,
\angle BAO=60^{\circ},~\angle BAC=2\angle BAO=120^{\circ}.