1819. Одна окружность описана около равностороннего треугольника ABC
, а вторая касается прямых AB
и AC
и первой окружности. Найдите отношение радиусов окружностей.
Ответ. 3:2
, 1:2
или 1:6
.
Указание. Рассмотрите три возможных случая.
Решение. Пусть окружность радиуса R
с центром O
описана около равностороннего треугольника ABC
, а окружность радиуса r
с центром O_{1}
касается прямых AB
и AC
, причём прямой AB
— в точке D
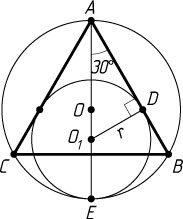
, а также внутренним образом касается первой окружности в точке E
(рис. 1). Тогда в прямоугольном треугольнике AO_{1}D
катет O_{1}D
лежит против угла DAO_{1}
, равного 30^{\circ}
. Поэтому
AO_{1}=2O_{1}D=2r,
а так как центры обеих окружностей лежат на биссектрисе угла BAC
, то
AO_{1}=AE-O_{1}E=2R-r.
Из уравнения 2R-r=2r
находим, что \frac{R}{r}=\frac{3}{2}
.
Пусть окружность радиуса r
с центром O_{1}
вписана в угол BAC
, касается продолжения стороны AB
в точке D
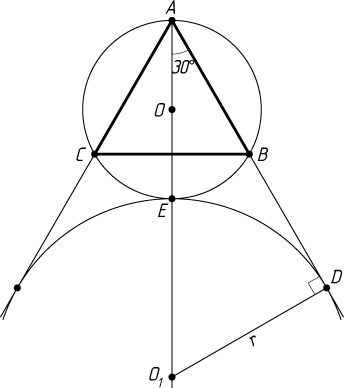
, а также внешним образом касается первой окружности в точке E
(рис. 2). Тогда
AO_{1}=2O_{1}D=2r,~AO_{1}=AE+O_{1}E=2R+r.
Из уравнения 2R+r=2r
находим, что \frac{R}{r}=\frac{1}{2}
.
Пусть теперь окружность радиуса r
с центром O_{1}
вписана в угол, смежный с углом BAC
, касается продолжения стороны AB
в точке D
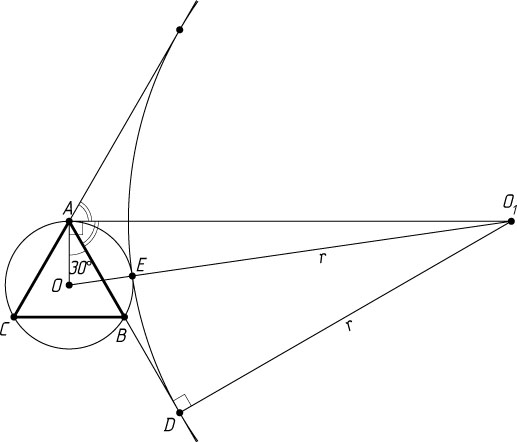
, а также внешним образом касается первой окружности в точке E
(рис. 3). Тогда \angle OAO_{1}=90^{\circ}
как угол между биссектрисами смежных углов,
AO_{1}=\frac{O_{1}D}{\sin\angle DAO_{1}}=\frac{r}{\sin60^{\circ}}=\frac{2r}{\sqrt{3}},~OO_{1}=OE+EO_{1}=R+r.
По теореме Пифагора OO_{1}^{2}=OA^{2}+AO_{1}^{2}
, или (R+r)^{2}=R^{2}+\left(\frac{2r}{\sqrt{3}}\right)^{2}
. Из этого уравнения находим, что \frac{R}{r}=\frac{1}{6}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.19, с. 68


