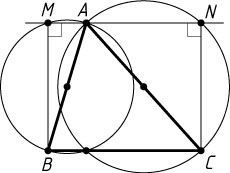
1822. Через вершину A
остроугольного треугольника ABC
проведена прямая, параллельная стороне BC
, равной a
, и пересекающая окружности, построенные на сторонах AB
и AC
как на диаметрах, в точках M
и N
, отличных от A
. Найдите MN
.
Ответ. a
.
Указание. \angle AMB=\angle ANC=90^{\circ}
.
Решение. Поскольку точка M
лежит на окружности с диаметром AB
, то \angle AMB=90^{\circ}
. Аналогично \angle ANC=90^{\circ}
. Значит, противоположные стороны четырёхугольника BMNC
попарно параллельны. Следовательно, MN=BC=a
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10.4, с. 76
