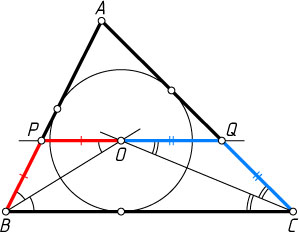
1823. Каждая из трёх прямых, параллельных сторонам и проходящих через центр вписанной окружности треугольника, отсекают от него некоторый треугольник. Докажите, что сумма периметров отсечённых треугольников вдвое больше периметра исходного треугольника.
Указание. Докажите, что периметр каждого из отсечённых треугольников равен сумме двух сторон данного треугольника.
Решение. Пусть прямая, проходящая через центр O
вписанной окружности треугольника ABC
параллельно стороне BC
, пересекает стороны AB
и AC
соответственно в точках P
и Q
. Поскольку O
— точка пересечения биссектрис треугольника ABC
, луч BO
— биссектриса угла B
, поэтому
\angle BOP=\angle OBC=\angle OBP,
значит, PO=BP
. Аналогично QO=QC
. Следовательно,
AP+PQ+AQ=AP+PB+AQ+QC=AB+AC.
Аналогично докажем, что периметр каждого из двух других отсечённых треугольников равен сумме двух соответствующих сторон треугольника ABC
. Осталось почленно сложить три полученных равенства.