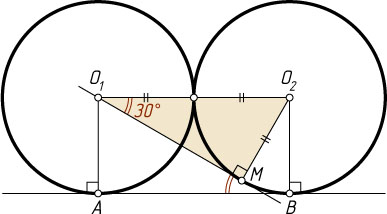
1825. Даны две равные касающиеся окружности. Под каким углом пересекаются прямые, одна из которых касается этих окружностей в разных точках, а вторая проходит через центр одной из окружностей и касается другой?
Ответ. 30^{\circ}
.
Указание. Расстояние между центрами данных окружностей вдвое больше их радиуса.
Решение. Пусть прямая, проходящая через центр O_{1}
первой окружности, касается второй окружности с центром O_{2}
в точке M
. В прямоугольном треугольнике O_{1}MO_{2}
гипотенуза O_{1}O_{2}
вдвое больше катета O_{2}M
, поэтому \angle MO_{1}O_{2}=30^{\circ}
. Если окружности касаются некоторой прямой в различных точках A
и B
, то прямая O_{1}O_{2}
параллельна общей касательной. Следовательно, прямые O_{1}M
и AB
пересекаются под углом 30^{\circ}
.