1835. Из произвольной точки основания равнобедренного треугольника с боковой стороной, равной a
, проведены прямые, параллельные боковым сторонам. Найдите периметр получившегося четырёхугольника.
Ответ. 2a
.
Указание. Получившийся четырёхугольник — параллелограмм.
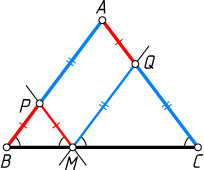
Решение. Пусть прямая, проходящая через произвольную точку M
основания BC
равнобедренного треугольника ABC
параллельно боковой стороне AC
, пересекает боковую сторону AB
в точке P
, а прямая, проходящая через точку M
параллельно боковой стороне AB
, пересекает боковую сторону AC
в точке Q
. Тогда четырёхугольник APMQ
— параллелограмм, так как его противоположные стороны попарно параллельны. Треугольники BPM
и CQM
равнобедренные, так как
\angle PMB=\angle ACB=\angle PBM,~\angle QMC=\angle ABC=\angle QCM.
Значит, PM=BP
и QM=QC
. Следовательно,
AP+PM+QM+AQ=2(AP+PM)=2(AP+PB)=2AB=2a.