1865. Найдите расстояние от центра ромба до его стороны, если острый угол ромба равен 30^{\circ}
, а сторона равна 4.
Ответ. 1.
Указание. Опустите перпендикуляр из вершины тупого угла ромба на одну из противолежащих сторон.
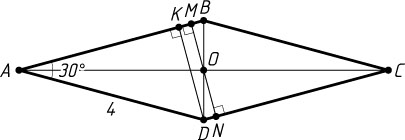
Решение. Пусть O
— центр ромба ABCD
, в котором \angle BAD=30^{\circ}
. Опустим перпендикуляр OM
из точки O
на сторону AB
и продолжим его до пересечения со стороной CD
в точке N
. Тогда MN\perp CD
.
Пусть DK
— перпендикуляр, опущенный из вершины D
на сторону AB
. В прямоугольном треугольнике AKD
отрезок DK
— катет, лежащий против угла в 30^{\circ}
. Поэтому DK=\frac{1}{2}AD=2
. Следовательно,
OM=\frac{1}{2}MN=\frac{1}{2}DK=1.
