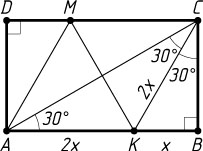
1867. На сторонах AB
и CD
прямоугольника ABCD
взяты точки K
и M
так, что AKCM
— ромб. Диагональ AC
образует со стороной AB
угол 30^{\circ}
. Найдите сторону ромба, если наибольшая сторона прямоугольника ABCD
равна 3.
Ответ. 2.
Указание. AK=KC
, \angle BCK=30^{\circ}
.
Решение. В прямоугольном треугольнике ABC
катет AB
лежит против угла в 60^{\circ}
, поэтому AB\gt BC
, т. е. AB
и DC
— большие стороны прямоугольника ABCD
. В равнобедренном треугольнике AKC
углы при основании AC
равны, поэтому
\angle BCK=\angle ACB-\angle ACK=60^{\circ}-30^{\circ}=30^{\circ}.
Обозначим BK=x
. Тогда
AK=CK=2BK=2x,~AB=AK+BK=3x=3,
откуда x=1
. Следовательно,
AK=KC=MC=AM=2.
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 13, с. 150
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.7, с. 23
