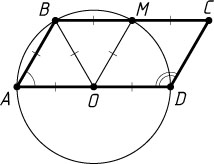
1870. Окружность, построенная на стороне AD
параллелограмма ABCD
как на диаметре, проходит через вершину B
и середину стороны BC
. Найдите углы параллелограмма.
Ответ. 60^{\circ}
, 120^{\circ}
.
Указание. Пусть O
— середина стороны AD
. Докажите, что треугольник ABO
— равносторонний.
Решение. Пусть O
— середина стороны AD
, M
— середина стороны BC
. Окружность с центром O
проходит через точки A
, B
и M
, а также BM=AO
и BM\parallel AO
, поэтому AB=OM=OB=OA
. Значит, треугольник ABO
— равносторонний. Следовательно,
\angle BAD=60^{\circ},~\angle ABC=120^{\circ}.
