1874. Прямая имеет с параллелограммом ABCD
единственную общую точку B
. Вершины A
и C
удалены от этой прямой на расстояния, равные a
и b
. На какое расстояние удалена от этой прямой вершина D
?
Ответ. a+b
.
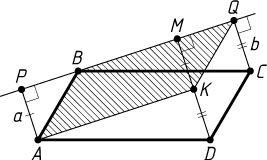
Решение. Пусть P
, M
и Q
— проекции точек соответственно A
, D
и C
на указанную прямую. Если прямая, проходящая через точку Q
параллельно CD
, пересекает отрезок DM
в точке K
, то CDKQ
— параллелограмм. Поэтому
KQ=CD=AB,~KQ\parallel CD\parallel AB,
значит, ABQK
— также параллелограмм. Прямоугольные треугольники APB
и KMQ
равны по гипотенузе и острому углу, поэтому MK=AP=a
. Следовательно,
DM=MK+DK=a+b.
Примечание. Аналогично можно доказать, что если указанная прямая пересекает сторону AD
(или CD
), то расстояние от вершины D
до этой прямой равно |a-b|
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.19, с. 24
