1901. В выпуклом четырёхугольнике ABCD
отрезок, соединяющий середины диагоналей, равен отрезку, соединяющему середины сторон AD
и BC
. Найдите угол, образованный продолжением сторон AB
и CD
.
Ответ. 90^{\circ}
.
Указание. Четырёхугольник с вершинами в серединах отрезков AB
, AC
, CB
и BD
— прямоугольник.
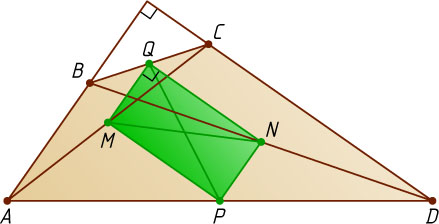
Решение. Пусть M
и N
— середины диагоналей соответственно AC
и BD
данного четырёхугольника ABCD
, P
и Q
— середины сторон соответственно AD
и BC
, MN=PQ
.
Отрезки MQ
и PN
— средние линии треугольников ABC
и ABD
, поэтому MQ\parallel AB
, MQ=\frac{1}{2}AB
, PN\parallel AB
, PN=\frac{1}{2}AB
, значит, MQ\parallel PN
и MQ=PN
. Следовательно, четырёхугольник MPNQ
— параллелограмм, а так как его диагонали MN
и PQ
равны, то это прямоугольник.
Отрезок NQ
— средняя линия треугольника CBD
, поэтому NQ\parallel CD
. Прямые MQ
и NQ
перпендикулярны, значит, перпендикулярны и соответственно параллельные им прямые AB
и CD
, следовательно, угол, образованный продолжением сторон AB
и CD
равен 90^{\circ}
.
Источник: Вступительный экзамен на химический факультет МГУ. — 1977, вариант 4, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 52
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.21, с. 24
