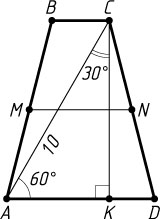
1927. Диагональ равнобедренной трапеции равна 10 и образует угол, равный 60^{\circ}
, с основанием трапеции. Найдите среднюю линию трапеции.
Ответ. 5.
Указание. Опустите перпендикуляр из вершины меньшего основания на большее.
Решение. Из вершины C
меньшего основания равнобедренной трапеции ABCD
опустим перпендикуляр CK
на большее основание. Тогда отрезок AK
равен полусумме оснований трапеции. В прямоугольном треугольнике AKC
катет AK
лежит против угла в 30^{\circ}
, поэтому AK=\frac{1}{2}AC=5
. Поскольку средняя линия MN
трапеции также равна полусумме оснований, то
MN=AK=5.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.6, с. 30
