1928. Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Решение. Первый способ. Пусть M
и N
— середины боковых сторон соответственно AB
и CD
трапеции ABCD
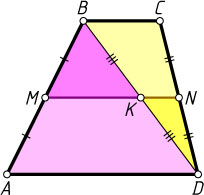
(рис. 1). Соединим точки M
и N
с серединой K
диагонали BD
. Тогда MK
и NK
— средние линии треугольников ABD
и BDC
, поэтому
MK\parallel AD\parallel BC\parallel NK,
а так как через точку, не лежащую на прямой, можно провести не более одной прямой, параллельной данной, то точки M
, K
и N
лежат на одной прямой. Значит, MN\parallel AD\parallel BC
.
В то же время,
MN=MK+KN=\frac{1}{2}AD+\frac{1}{2}BC=\frac{AD+BC}{2}.
Второй способ. Пусть M
и N
— середины боковых сторон соответственно AB
и CD
трапеции ABCD
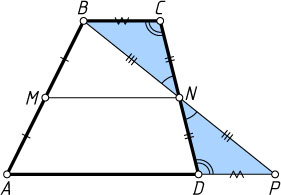
(рис. 2). На продолжении отрезка BN
за точку N
отложим отрезок NP
, равный BN
. Треугольники DNP
и CNB
равны по двум сторонам и углу между ними, поэтому DP=BC
и \angle NDP=\angle NCB
. Значит, DP\parallel BC
, а так как через точку, не лежащую на прямой, можно провести не более одной прямой, параллельной данной, то точки A
, D
и P
лежат на одной прямой. Поэтому AP=AD+DP
.
Отрезок MN
— средняя линия треугольника ABP
, поэтому
MN=\frac{1}{2}AP=\frac{AD+DP}{2}=\frac{AD+BC}{2}.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 34, с. 64

