1929. Расстояния от концов диаметра окружности до некоторой касательной равны a
и b
. Найдите радиус окружности.
Ответ. \frac{a+b}{2}
.
Указание. Примените теорему о средней линии трапеции.
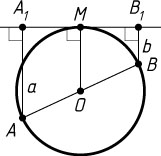
Решение. Пусть прямая касается окружности с центром O
в точке M
. Опустим перпендикуляры AA_{1}
и BB_{1}
из концов диаметра AB
на эту прямую, AA_{1}=a
, BB_{1}=b
. Поскольку OM\perp A_{1}B_{1}
, то
AA_{1}\parallel OM\parallel BB_{1},
а так как O
— середина AB
, то OM
— средняя линия трапеции AA_{1}B_{1}B
(или прямоугольника, если a=b
). Следовательно,
OM=\frac{1}{2}(AA_{1}+BB_{1})=\frac{a+b}{2}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.11, с. 60
