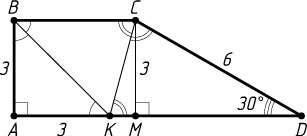
1932. Меньшая боковая сторона прямоугольной трапеции равна 3, а большая образует угол 30^{\circ}
, с одним из оснований. Найдите это основание, если на нём лежит точка пересечения биссектрис углов при другом основании.
Ответ. 9.
Указание. Если биссектриса угла B
при основании BC
трапеции ABCD
пересекает основание AD
в точке K
, то треугольник ABK
— равнобедренный.
Решение. Пусть BC
и AD
— основания прямоугольной трапеции ABCD
, AB
и CD
— боковые стороны (AB\lt CD
), \angle ADC=30^{\circ}
, K
— точка пересечения биссектрис углов трапеции при вершинах B
и C
.
Поскольку \angle BKM=\angle KBC=\angle KBA
, то треугольник ABK
— равнобедренный, поэтому AK=AB=3
. Аналогично докажем, что DK=CD
.
Пусть CM
— высота трапеции. Из прямоугольного треугольника CMD
находим, что CD=2CM=2AB=6
. Следовательно,
AD=AK+KD=AK+CD=3+6=9.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.8, с. 30
