1941. Две окружности касаются внешним образом в точке K
. Одна прямая касается этих окружностей в различных точках A
и B
, а вторая — соответственно в различных точках C
и D
. Общая касательная к окружностям, проходящая через точку K
, пересекается с этими прямыми в точках M
и N
. Найдите MN
, если AC=a
, BD=b
.
Ответ. \frac{a+b}{2}
.
Указание. ABDC
— равнобедренная трапеция (или прямоугольник), а MN
— средняя линия.
Решение. Пусть прямые AB
и CD
пересекаются в точке P
. Углы при основаниях равнобедренных треугольников PAC
и PBD
равны, поэтому AC\parallel BD
. Значит, ABDC
— равнобедренная трапеция. Поскольку MA=MK=MB
, то M
— середина боковой стороны AB
. Аналогично, N
— середина боковой стороны CD
, значит, MN
— средняя линия трапеции ABDC
. Следовательно,
MN=\frac{1}{2}(AC+BD)=\frac{a+b}{2}.
Если AB\parallel CD
, то ABDC
— прямоугольник. В этом случае MN=AC=BD
.
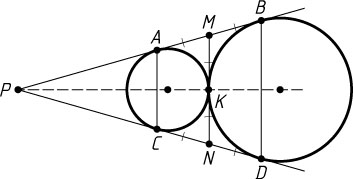
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.15, с. 68
