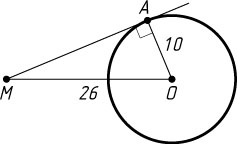
1957. Прямая, проходящая через точку M
, удалённую от центра окружности радиуса 10 на расстояние, равное 26, касается окружности в точке A
. Найдите AM
.
Ответ. 24.
Указание. Касательная перпендикулярна радиусу, проведённому в точку касания.
Решение. Пусть O
— центр окружности. Касательная перпендикулярна радиусу, проведённому в точку касания, поэтому треугольник AMO
— прямоугольный. По теореме Пифагора
AM=\sqrt{OM^{2}-OA^{2}}=\sqrt{26^{2}-10^{2}}=\sqrt{(26-10)(26+10)}=\sqrt{16\cdot36}=24.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.6, с. 60
