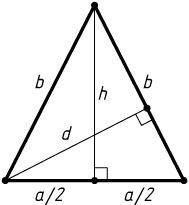
1969. Найдите высоту равнобедренного треугольника, проведённую к боковой стороне, если основание равно a
, а боковая сторона равна b
.
Ответ. \frac{a\sqrt{4b^{2}-a^{2}}}{2b}
.
Указание. Произведение искомой высоты на боковую сторону равно произведению основания на проведённую к нему высоту.
Решение. Пусть d
— искомая высота, h
— высота, опущенная на основание данного равнобедренного треугольника. Тогда
h=\sqrt{b^{2}-\left(\frac{a}{2}\right)^{2}}=\frac{\sqrt{4b^{2}-a^{2}}}{2}.
С одной стороны, площадь треугольника равна \frac{1}{2}ah
, с другой — \frac{1}{2}bd
. Из равенства ah=bd
находим, что
d=\frac{ah}{b}=\frac{a\sqrt{4b^{2}-a^{2}}}{2}:b=\frac{a\sqrt{4b^{2}-a^{2}}}{2b}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 35
