1977. Найдите диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12, если известно, что центр её описанной окружности лежит на большем основании.
Ответ. 8\sqrt{5}
, 4\sqrt{5}
.
Указание. Опустите перпендикуляр из центра окружности на меньшее основание трапеции.
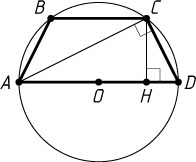
Решение. Первый способ. Пусть O
— центр окружности, описанной около равнобедренной трапеции ABCD
с основаниями AD=20
и BC=12
. По условию O
— середина AD
. Опустим перпендикуляр OM
из центра окружности на основание BC
. Так как диаметр, перпендикулярный хорде, делит её пополам, то M
— середина BC
. Из прямоугольного треугольника OMC
находим, что
OM=\sqrt{OC^{2}-MC^{2}}=\sqrt{100-36}=\sqrt{64}=8.
Пусть CH
— перпендикуляр, опущенный из вершины C
на основание AD
. Тогда
CH=OM=8,~DH=\frac{1}{2}(AD-BC)=4,
поэтому
AB=CD=\sqrt{CH^{2}+DH^{2}}=\sqrt{64+16}=\sqrt{80}=4\sqrt{5},
BD=AC=\sqrt{AH^{2}+CH^{2}}=\sqrt{16^{2}+8^{2}}=\sqrt{320}=8\sqrt{5}.
Второй способ. Пусть O
— центр окружности, описанной около равнобедренной трапеции ABCD
с основаниями AD=20
и BC=12
, CH
— перпендикуляр, опущенный из вершины C
на основание AD
. Тогда
AH=\frac{AD+BC}{2}=16,~DH=\frac{AD-BC}{2}=4.
Поскольку точка C
лежит на окружности с диаметром AD
, то \angle ACD=90^{\circ}
, поэтому CH
— высота прямоугольного треугольника ACD
, проведённая из вершины прямого угла. Следовательно,
CD^{2}=DH\cdot AD=4\cdot20,~AC^{2}=AH\cdot AD=16\cdot20.
Таким образом, AB=CD=4\sqrt{5}
, AC=8\sqrt{5}
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — N.10.002
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.21, с. 31
