1980. Отрезок, соединяющий центры двух пересекающихся окружностей, делится их общей хордой на отрезки, равные 5 и 2. Найдите общую хорду, если известно, что радиус одной окружности вдвое больше радиуса другой.
Ответ. 2\sqrt{3}
.
Указание. Отрезок, соединяющий точки пересечения окружностей, перпендикулярен линии центров.
Решение. Пусть окружности с центрами O_{1}
и O_{2}
и радиусами соответственно r
и 2r
пересекаются в точках A
и B
, а отрезки O_{1}O_{2}
и AB
— в точке K
. Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде, поэтому треугольники AO_{1}K
и AO_{2}K
прямоугольные. Поскольку AO_{1}\lt AO_{2}
, то KO_{1}\lt KO_{2}
. Значит, KO_{1}=2
и KO_{2}=5
.
По теореме Пифагора
AO^{2}_{1}-KO^{2}_{1}=AO^{2}_{2}-KO^{2}_{2},~\mbox{или}~r^{2}-4=4r^{2}-25,
откуда находим, что r=\sqrt{7}
. Следовательно,
AB=2AK=2\sqrt{r^{2}-4}=2\sqrt{7-4}=2\sqrt{3}.
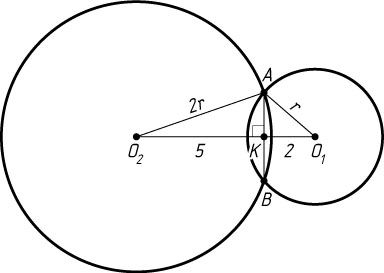
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10.3, с. 76
