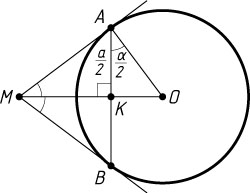
1981. Из точки M
проведены касательные MA
и MB
к окружности с центром O
(A
и B
— точки касания). Найдите радиус окружности, если \angle AMB=\alpha
и AB=a
.
Ответ. \frac{a}{2\cos\frac{\alpha}{2}}
.
Указание. Отрезок OM
перпендикулярен хорде AB
, делит её пополам, а \angle OAB=\frac{\alpha}{2}
.
Решение. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, поэтому \angle AMO=\frac{\alpha}{2}
. Отрезок OM
перпендикулярен хорде AB
, проходит через её середину K
, а \angle OAK=\angle AMO=\frac{\alpha}{2}
. Из прямоугольного треугольника AOK
находим, что
OA=\frac{AK}{\cos\angle OAK}=\frac{\frac{a}{2}}{\cos\frac{\alpha}{2}}=\frac{a}{2\cos\frac{\alpha}{2}}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.8, с. 60
