1989. На боковой стороне равнобедренного треугольника как на диаметре построена окружность, делящая вторую боковую сторону на отрезки, равные a
и b
. Найдите основание треугольника.
Ответ. \sqrt{2a(a+b)}
или \sqrt{2b(a+b)}
.
Указание. Пусть окружность, построенная как на диаметре на боковой стороне AB
равнобедренного треугольника ABC
, пересекает боковую сторону AC
в точке K
. Тогда \angle AKB=90^{\circ}
.
Решение. Первый способ. Пусть окружность, построенная как на диаметре на боковой стороне AB
равнобедренного треугольника ABC
, пересекает боковую сторону AC
в точке K
, причём CK=a
, AK=b
. Тогда \angle AKB=90^{\circ}
. Из прямоугольного треугольника AKB
по теореме Пифагора находим, что
BK=\sqrt{AB^{2}-AK^{2}}=\sqrt{(a+b)^{2}-b^{2}}=\sqrt{a(2b+a)},
а из прямоугольного треугольника BKC
—
BC=\sqrt{BK^{2}+CK^{2}}=\sqrt{a(2b+a)+a^{2}}=\sqrt{2a(a+b)}.
Второй способ. Пусть окружность, построенная как на диаметре на боковой стороне AB
равнобедренного треугольника ABC
, пересекает боковую сторону AC
в точке K
, а основание BC
— в точке M
, причём CK=a
, AK=b
. Тогда \angle AMB=90^{\circ}
, т. е. AM
— высота равнобедренного треугольника, проведённая к основанию. Значит, M
— середина BC
.
Из точки C
к окружности проведены две секущие, поэтому
CM\cdot CB=CK\cdot CA,~\mbox{или}~\frac{1}{2}CB^{2}=a(a+b),
откуда CB=\sqrt{2a(a+b)}
.
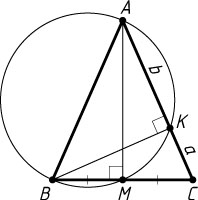
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.9, с. 93
