1996. Основания равнобедренной трапеции равны a
и b
(a\gt b
), острый угол равен 45^{\circ}
. Найдите площадь трапеции.
Ответ. \frac{a^{2}-b^{2}}{4}
.
Указание. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований.
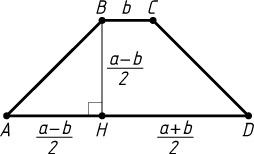
Решение. Из вершины B
меньшего основания BC
равнобедренной трапеции ABCD
опустим перпендикуляр BH
на её большее основание AD
. Тогда
BH=AH=\frac{1}{2}(AD-BC)=\frac{a-b}{2}.
Следовательно,
S_{ABCD}=\frac{1}{2}(AD+BC)\cdot BH=\frac{a+b}{2}\cdot\frac{a-b}{2}=\frac{a^{2}-b^{2}}{4}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.11, с. 30
