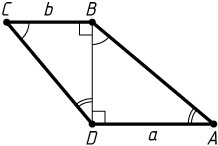
2018. В трапеции ABCD
меньшая диагональ BD
перпендикулярна к основаниям AD
и BC
, сумма острых углов A
и C
равна 90^{\circ}
. Основания AD=a
, BC=b
. Найдите боковые стороны трапеции.
Ответ. \sqrt{a(a+b)}
, \sqrt{b(a+b)}
.
Указание. Треугольники ABD
и DCB
подобны.
Решение. Поскольку
\angle BCD=90^{\circ}-\angle A,~\angle ABD=90^{\circ}-\angle A,
то \angle BCD=\angle ABD
и треугольники ABD
и DCB
подобны по двум углам. Следовательно,
\frac{BC}{BD}=\frac{BD}{AD}.
Поэтому
BD=\sqrt{BC\cdot AD}=\sqrt{ab}.
Следовательно,
CD=\sqrt{BC^{2}+BD^{2}}=\sqrt{b^{2}+ab}=\sqrt{b(a+b)},
AB=\sqrt{BD^{2}+AD^{2}}=\sqrt{a^{2}+ab}=\sqrt{a(a+b)}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 78, с. 62
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 108
